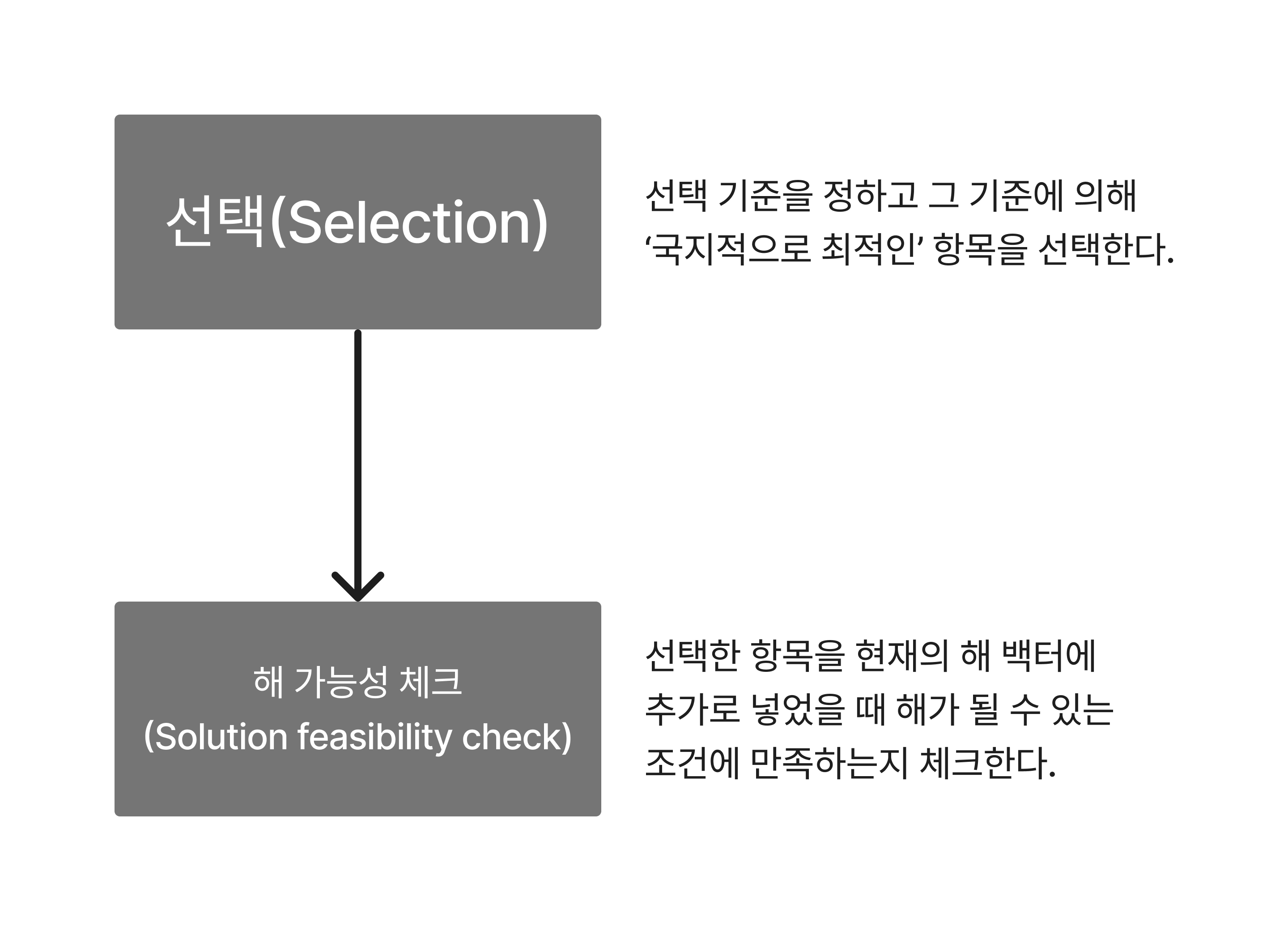
욕심쟁이 기법
- 단계별로 연속된 선택을 함으로써 문제에 대한 해 백터(solution vector)를 구해나간다. 또한 각 단계별 선택은 전체적으로 최적인(Globally optimal) 선택을 하는 것이 아니라, 정해진 어떠한 선택 기준에 의해 그 단계에서 가장 최선인 선택, 즉 국지적으로 최적인(Locally optimal) 선택을 하는 것이다.
동전 교환 문제
- 단순 반복문 사용하여 동전의 개수를 최소화 하는 문제
- 가장 액수가 큰 동전을 차감하는 반복문을 사용한다.
테이프 장치 최적 공간 배정 문제
- 모든 프로그램에 대한 평균 검색 시간을 최소화하는 프로그램의 저장 순서를 결정하는 문제
- 가장 용량이 작은 프로그램을 순차적으로 할당한다.
분수 배낭 문제
- 각 물건의 무게를 Xi라고 할 때, Xi의 값이 0또는 1인 경우를 0-1 배낭문제라 하며, 이는 다항시간 알고리즘이 존재하지 않는 어려운 문제이다.
- 각 물건의 무게가 만일, 0 <= Xi <= 1인 경우를 분수 배낭 문제라하며 이는 물건 i를 분할해서 가져갈 수 있는 알고리즘이다.
- 문제의 전략은 최대 이윤을 냄과 동시에 무조건 배낭을 꽉 채우는 것이다. 따라서, 단위 무게당 가장 큰 이윤을 낼 수 있는 물건을 먼저 넣은 뒤, 순차적으로 이윤이 큰 물건을 남아 있는 배낭에 채운다.
최소 스패닝 트리(Minimum spanning tree)

- 부분 그래프를 구성하는 모든 에지들의 가중치 합을 부분 그래프의 가중치라고 정의하면, 최소 스패닝 트리란, 스패닝 트리 중에서 최소의 가중치를 갖는 스패닝 트리이다.
- 스패닝 트리의 최적의 해를 항상 구하는 알고리즘은 대표적으로 '프림 알고리즘' 과 '크러스컬 알고리즘'이 있다.

프림 알고리즘(Prim Algorithm)
- 프림 알고리즘은 가중치 그래프 G에서 임의의 한 정점을 선택하여 시작한다.
그리고, 각 반복 과정마다 그때까지 구성된 최소 스패닝 트리의 부분에 새로운 정점과 에지를 선택하여 첨가한다. - 알고리즘이 진행되는 동안 G의 각 정점들은 다음과 같은 세 가지의 범주로 나누어진다.
- 트리 정점: 지금까지 구성된 스패닝 트리 내의 정점들의 집합
- 인접 정점: 트리 정점에 인접해 있는 정점들의 집합
- 나머지 정점: 트리 정점과 인접 정점을 제외한 그래프 나머지 정점들의 집합

- 프림 알고리즘에서는 MST의 후보가 될 간선을 담을 우선순위 큐가 필요하다. 이때, 우선순위 큐는 최소의 비용을 가지는 경로가 우선순위를 갖게 한다.
- 그래프의 랜덤한 노드를 선택한다.
- 선택된 노드에 연결된 모든 간선을 우선순위 큐에 삽입한다.
- 우선순위 큐에서 값을 하나 뺀다. 이때, 가중치가 가장 작은 값이 빠질 것이다.
- 트리가 순회하지 않는 선에서, 위 과정을 정점의 개수가 N개일때, 간선이 N-1개가 될 때까지 반복한다.
#include <iostream>
#include <queue>
using namespace std;
class Data
{
private:
int e;
int val;
public:
Data(int a, int b) : e(a), val(b)
{ }
bool operator<(const Data &d) const
{
return val > d.val;
}
}
int v,e,res = 0;
bool ch[1001];
priority_queue<Data> pQ;
vector<Data> graph[1001];
int main(void)
{
// Build G
// Start with 1
pQ.push(Data(1,0));
while(!pQ.empty())
{
Data temp = pQ.top();
pQ.pop();
int e = temp.e;
int val = temp.val;
if(ch[e] == false)
{
ch[e] = 1;
res += val;
for(int i = 0; i < graph[e].size(); i++)
{
pQ.push(Data(grpah[e][i].e, graph[e][i].val));
}
}
}
return 0;
}- 단, 프림 알고리즘의 경우 시간복잡도가 O(n^2)이다. 이에반해 크러스컬 알고리즘의 경우 동일하게 최적의 해를 찾아주지만, 시간 복잡도가 O(elog2e)로 많은 차이가 나기 때문에 크러스컬 알고리즘이 선호된다.
- 프림 알고리즘은 작동 방식만 기억해두자
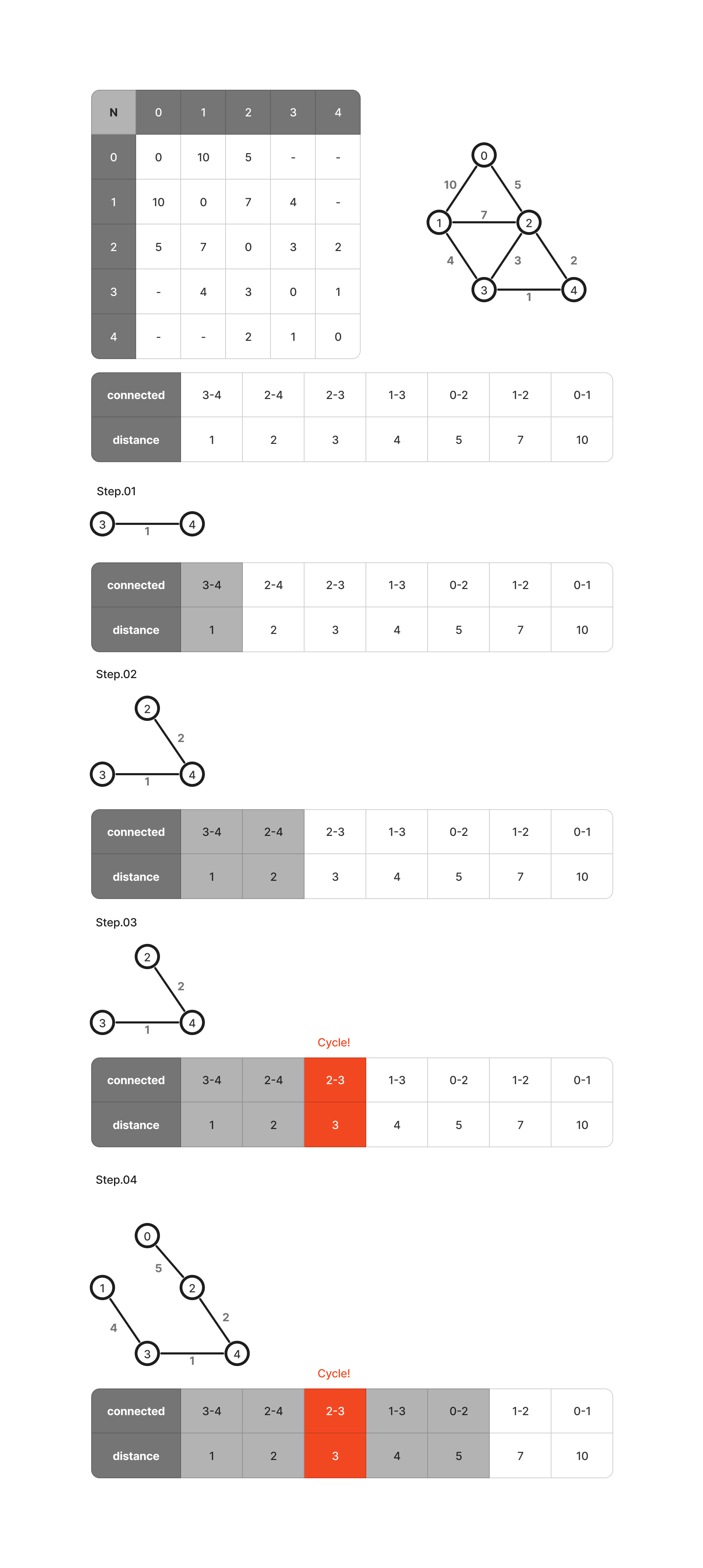
크러스컬 알고리즘(Kruskal Algorithm)
- 프림 알고리즘은 임의의 정점에서 시작하여 현재까지 구성된 트리 정점들과 인접 정점들 사이에 가장 작은 가중치를 갖는 에지들을 하나씩 선택하면서 스패닝 트리를 확장해나간다.
- 크러스컬 알고리즘의 경우 다음과 같은 동작을 취한다.
- 그래프 간선을 가중치 오름차순으로 정렬한다.
- 가중치가 가장 낮은 간선을 선택한다.
- 차례로 가중치가 낮은 간선을 선택하되, 만일 사이클이 형성된다면 해당 간선을 버린다.
- 위 과정을 반복하여 만일 간선의 개수가 (정점의 개수 n) n-1개가 된다면 작동을 멈춘다.
- 사이클을 판단하는 기준에는 Union & Find를 활용한다. 자세한 내용은 참고(https://waterglass0105.tistory.com/63)
- 코드로 구현하면 다음과 같다.
#include <iostream>
#include <algorithm>
#include <vector>
#define NODE 5
int arr[NODE];
class Edge
{
public:
int node[2];
int distance;
Edge(int a, int b, int distance)
{
this->node[0] = a;
this->node[1] = b;
this->distance = distance;
}
bool operator<(Edge &edge)
{
return this->distance < edge.distance;
}
}
// 부모 노드 탐색
int find(int x)
{
if(arr[x] == x)
return x;
return arr[x] = find(arr[x]);
}
// 두 노드를 작은 값을 기준으로 연결해준다.
void merge(int x, int y)
{
x = find(x);
y = find(y);
if(x < y) arr[y] = x;
else arr[x] = y;
}
// isUnion은 싸이클 존재 여부 또한 판별해준다.
bool isUnion(int x, int y)
{
x = find(x);
y = find(y);
if(x == y) return true;
return false;
}
int main(void)
{
vector<Edge> graph;
graph.push_back(Edge(0,1,10));
graph.push_back(Edge(0,2,5));
graph.push_back(Edge(1,2,7));
graph.push_back(Edge(1,3,4));
graph.push_back(Edge(2,3,3));
graph.push_back(Edge(2,4,2));
graph.push_back(Edge(3,4,1));
sort(v.begin(), v.end());
int sum = 0;
for(int i = 0; i < v.size(); ++i)
{
if(isUnion(v[i].node[0], v[i].node[1]))
{
sum+=v[i].distance;
merge(v[i].node[0], v[i].node[1]);
}
}
return 0;
}
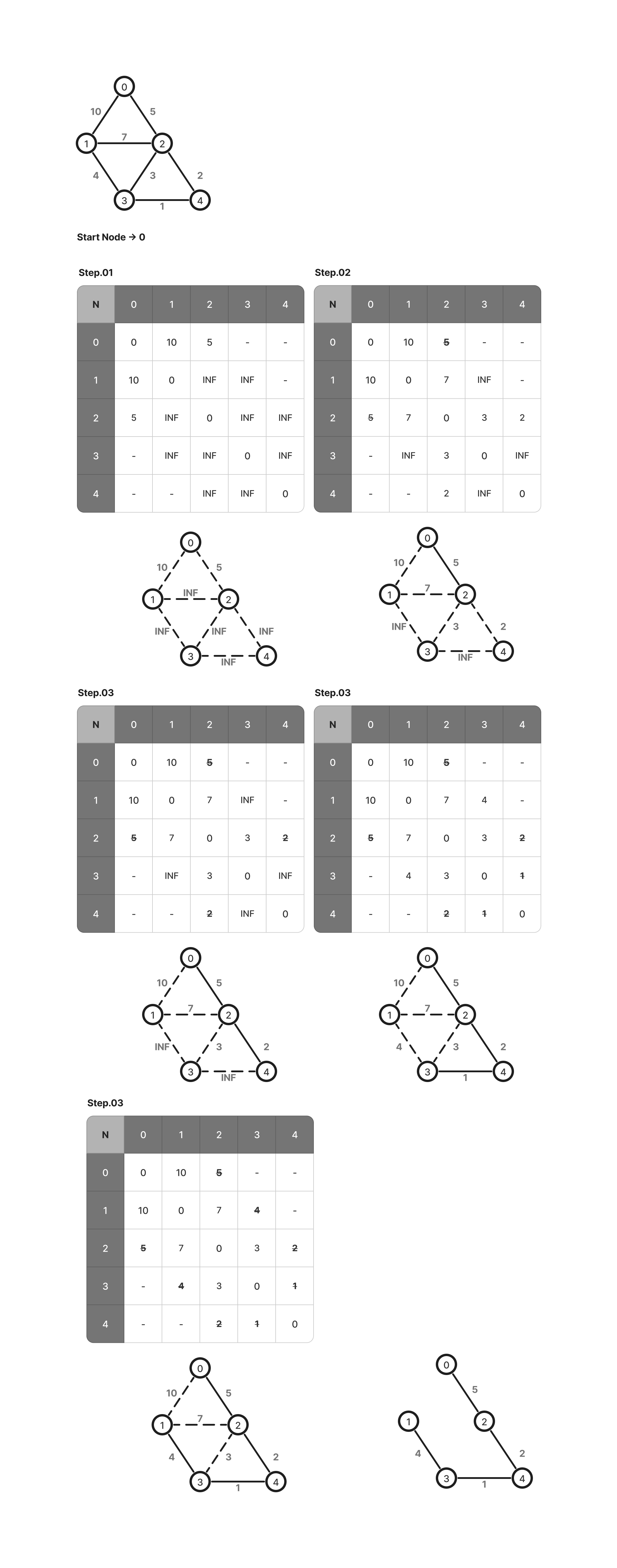
최단경로 문제 - 다익스트라(Dijkstra) 알고리즘
- V개의 정점과 음수가 아닌 E개의 간선을 가진 그래프 G에서 특정 출발 정점(S)에서 부터 다른 모든 정점까지의 최단 경로를 구하는 알고리즘으로 작동원리는 다음과 같다.
- 시작노드를 설정한다.이후, 시작 노드와 직접적으로 연결된 모든 정점들의 거리를 비교하여 업데이트 한 후, 시작 노드를 방문노드로 표시한다.
- 방문한 정점들과 연결되어 있는 정점들 중, 비용이 가장 적게 드는 정점을 선택, 해당 정점을 방문한 정점으로 표시한다.
- 2번 과정에서 선택된 정점을 1번과정을 거쳐 거리 비교 및 업데이트 한다.
- 2~3과정을 간선의 개수가 N-1(정점의 개수 N)이 될 때 까지 반복한다.
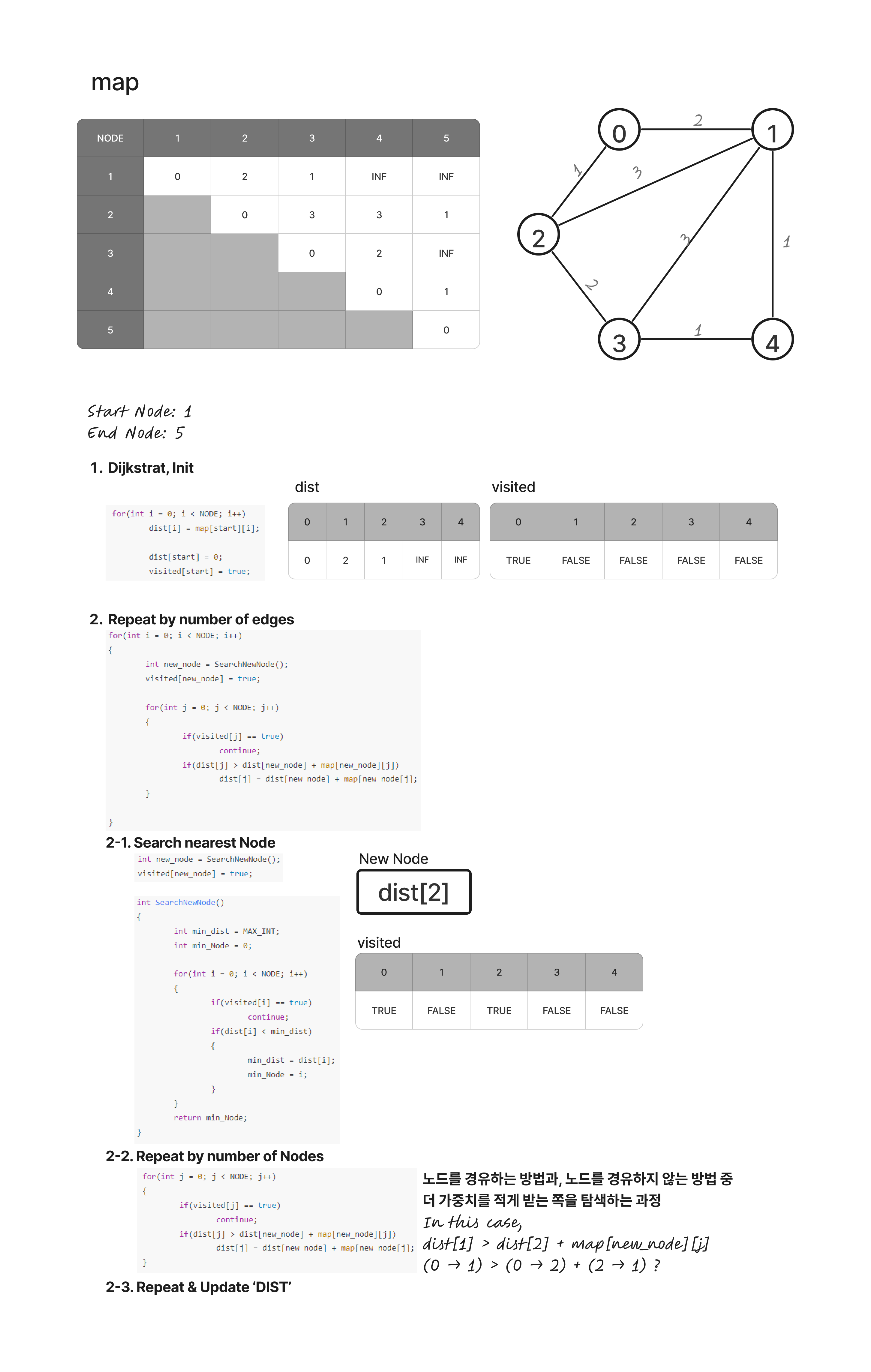
#define NODE
int map[NODE][NODE];
int dist[NODE];
bool visited[NODE] = {false, };
int SearchNewNode()
{
int min_dist = MAX_INT;
int min_Node = 0;
for(int i = 0; i < NODE; i++)
{
if(visited[i] == true)
continue;
if(dist[i] < min_dist)
{
min_dist = dist[i];
min_Node = i;
}
}
return min_Node;
}
void Dijkstra(int start)
{
for(int i = 0; i < NODE; i++)
dist[i] = map[start][i];
dist[start] = 0;
visited[start] = true;
for(int i = 0; i < NODE; i++)
{
int new_node = SearchNewNode();
visited[new_node] = true;
for(int j = 0; j < NODE; j++)
{
if(visited[j] == true)
continue;
if(dist[j] > dist[new_node] + map[new_node][j])
dist[j] = dist[new_node] + map[new_node[j];
}
}
}
- 작동원리를 추상화하면 다음과 같다.
- 다익스트라 알고리즘은 항상 최적의 결과를 내보이지만, 앞선 코드와 같이 순차탐색을 이용하면 시간 복잡도가 크게 올라가게 된다. (O(V^2))
- 이에, 순차 탐색이 아닌 우선순위 큐를 사용하여 다익스트라 알고리즘을 구현한다면, 우선순위 큐의 시간복잡도를 가진, 훨씬 효율적인 다익스트라 알고리즘이 완성된다. (O(ElogV))
- 작동원리는 위와 동일하나, 최단 거리가 가장 짧은 노드를 선택하기 위해 최소힙을 사용한다.
- C++에서 제공하는 queue의 priority_queue는 max_heap이다. 따라서, 이 과정또한 별도로 처리가 필요하다.
- 코드는 다음과 같다.
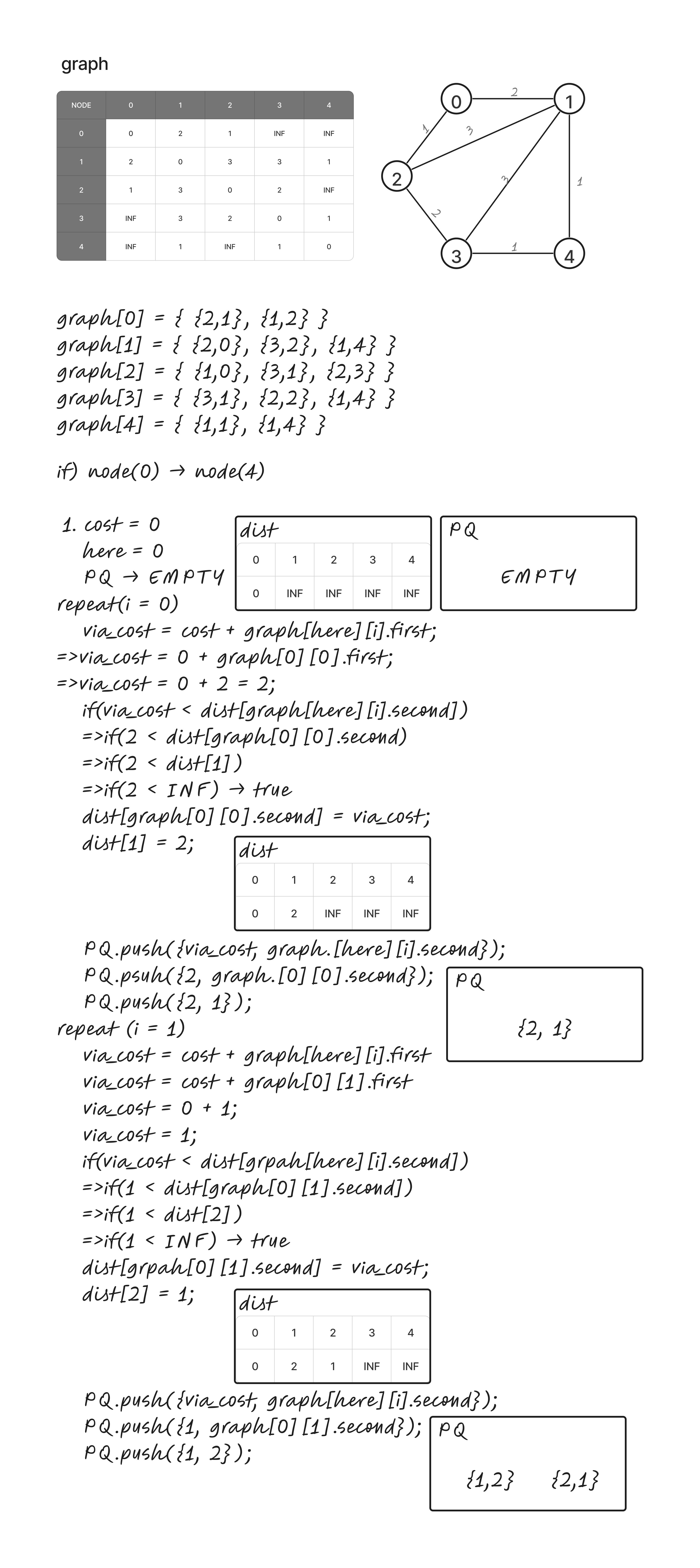
// distance, node
vector<pair<int, int>> graph[NODE];
/*
* graph
*
* [Table]
* NODE | 0 1 2 3 4
* ----------------------------
* 0 | 0 2 1 INF INF
* ----------------------------
* 1 | 2 0 3 3 1
* ----------------------------
* 2 | 1 3 0 2 INF
* ----------------------------
* 3 | INF 3 2 0 1
* ----------------------------
* 4 | INF 1 INF 1 0
*
* [vector]
* graph[0] = {{2,1}, {1,2}};
* graph[1] = {{2,0}, {3,2}, {1,4}};
* graph[2] = {{1,0}, {3,1}, {2,3}};
* graph[3] = {{3,1}, {2,2}, {1,4}};
* graph[4] = {{1,1}, {1,4}};
*/
int dist[NODE];
void dijkstra(int start)
{
/*
* priority_queue<pair<int, int>> pq;가 원형이다.
* 아래에서 사용한 코드는, 기존 Priority Queue가 MAX_HEAP이므로
* Dijkstra 알고리즘에서 요구되는 MIN_HEAP을 사용하기 위해 변형시켰다.
* Priority Queue의 경우, 첫 번째 원소를 먼저 비교하고, 만일 같다면 두 번째 원소를 기준으로 정렬한다.
*/
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> PQ;
PQ.push({ 0, start }); // 출발 지점과의 거리는 0이다.
dist[start] = 0; // 출발 노드를 기준으로 만들어진 최단거리가 저장되어 있는 배열, INF로 모두 초기화 되어있다.
// Priority Queue에 저장된 모든 노드가 사라질 때 까지 반복한다.
while (!PQ.empty())
{
/*
* Cost에는 PQ에 저장된 원소 중, distance가 가장 짧은 길이를 담는다.
* here에는 해당 원소의 노드를 담는다.
* 그 뒤, 해당 노드를 방문처리한다.
*/
int cost = PQ.top().first;
int here = PQ.top().second;
PQ.pop();
// 만일, 이미 최단거리의 정보를 가지고 있다면, 넘어간다.
if (dist[here] < cost) continue;
/*
* 현재 노드와 인접한 노드를 검사한다.
* 상단의 그래프를 참조하면, 출발점이 0이고 i가 0일때 3회 반복한다.
*/
for (int i = 0; i < graph[here].size(); i++)
{
/*
* via_cost는 here 노드를 경유하는 비용을 나타낸다.
* graph[here][i].first는 here노드와 인접한 노드들의 거리를 나타낸다.
*/
int via_cost = cost + graph[here][i].first;
/*
* 주변 노드들을 탐색하며, dist 값을 갱신한다.
* dist[graph[here][i].second]는 현재 노드와 인접 노드사이의 거리를 나타낸다.
* 즉, 만일 here를 경유하여 가는것이 더 빠르다면, dist를 갱신한다.
* 갱신 후 갱신된 노드를 PQ에 넣는다.
*/
if (via_cost < dist[graph[here][i].second])
{
dist[graph[here][i].second] = via_cost;
PQ.push({via_cost, graph[here][i].second});
}
}
}
}
허프만 코드
- 데이터를 효율적으로 압축하는데 사용하는 방법으로, 압축하고자 하는 문자열에서 자주 등장하는 문자는 짧은 비트로, 거의 등장하지 않는 문자는 긴 비트로 표현한다.
- 트리를 만들고, 해당 트리에 문자와 문자별 빈도수를 데이터로 가지는 노드를 삽입한다.
- 빈도수를 비교하여 가장 작은 빈도수를 가진 노드와 두 번째로 작은 빈도수를 가진 노드를 찾아 두 개의 빈도수를 합친 수로 새로운 노드를 하나 만들어준다.
- 만들어진 노드의 왼쪽 자식노드에는 가장 작은 빈도수를 가진 노드를 연결하고, 오른쪽 자식노드에는 두번째로 작은 빈도수를 가진 노드를 연결한다.
- 이 과정을 비교할 노드가 하나가 남을 때 까지 반복한다.
- 최종적으로 나온 결과에서, 왼쪽 간선에는 0을, 오른쪽 간선에는 1의 가중치를 둔다.
- 압축된 문자는 루트 노드에서 부터 해당 노드까지 가중치를 읽어들인다.
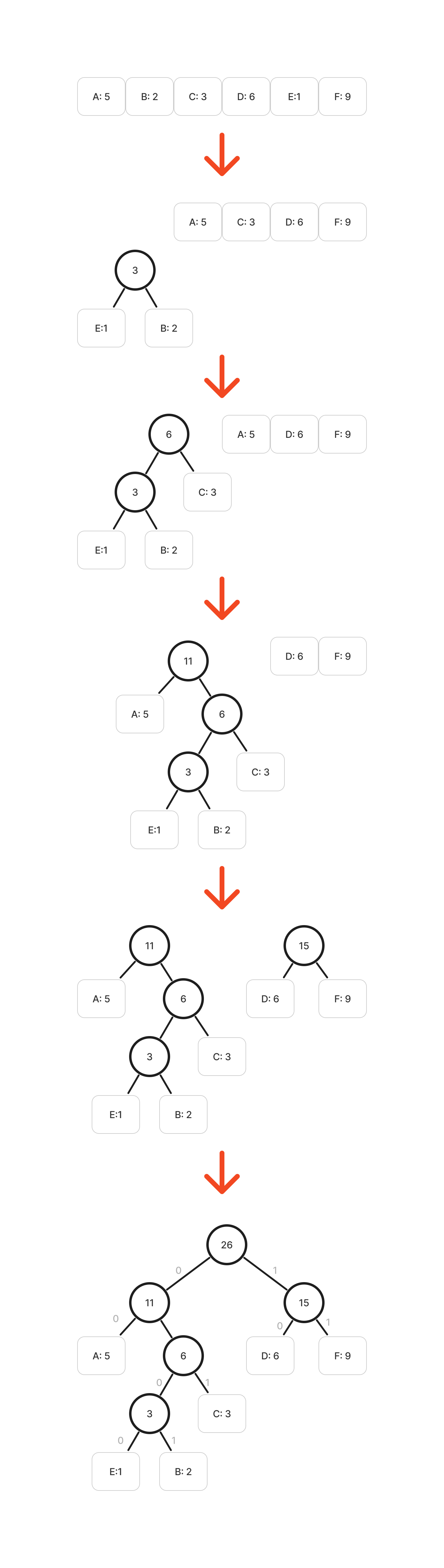
- 위 코드에서 E의 허프만 코드는 0100이된다.
public class Entry
{
private int frequency;
private String word;
private Entry left;
private Entry right;
private String code;
public Entry(int newFreq, String newVal, Entry l, Entry r, String newCode) : frequency(newFreq), word(newVal), left(l), right(r), code(newCode)
{ }
public int getFrequency() const
{
return frequency;
}
public int setFrequency(int frequency)
{
this.frequency = frequency;
}
public String getWord() const
{
return word;
}
public String setWord(String word) const
{
this.word = word;
}
public Entry getLeft() const
{
return left;
}
public void setLeft(Entry left)
{
this.left = left;
}
public Entry getRight() const
{
return right;
}
public void setRight(Entry Right)
{
this.right = right;
}
public string getCode() const
{
return code;
}
public setCode(string code)
{
this.code = code;
}
}
public class Huffman
{
private Entry[] harray; // [1]번째 부터 사용
private int size; // heap Size
public Huffman(Entry[] heapArray, int initialSize) // constructor
{
harray = heapArray;
size = initialSize;
}
private bool greater(int i, int j) // operator
{
return harray[i].getFrequency() > harray[j].getFrequency();
}
public Entry createTree() // Node가 최종적으로 1개가 될 때 까지 반복
{
while(size() > 1)
{
Entry e1 = deleteMin(); // Heap 에서 최소 빈도수를 가진 노드 제거
Entry e2 = deleteMin(); // Heap 에서 최소 빈도수를 가진 노드 제거
Entry temp = new Entry(e1.getFrequency() + e2.getFrequency(), e1.getWord() + e2.getWord(), e1,e2," "); // 빈도수 합, 단어 붙이기, 새로운 노드 생성
insert(temp); // 새 노드 힙 삽입
}
return deleteMin();
}
}https://velog.io/@junhok82/%ED%97%88%ED%94%84%EB%A7%8C-%EC%BD%94%EB%94%A9Huffman-coding
허프만 코딩(Huffman coding)
허프만 부호화 또는 허프만 코딩(Huffman coding)은 입력 파일의 문자 빈도 수를 가지고 최소힙을 이용하여 파일을 압축하는 과정이다. 허프만 코드(이진코드)는 Unix에서 파일압축에 사용되고, JPEG
velog.io
'Study > Algorithm' 카테고리의 다른 글
| P/NP & Approximation Algorithm (0) | 2023.11.16 |
|---|---|
| [Algorithm] Dynamic Programming (0) | 2023.10.25 |
| [Algorithm] Divide & Conquer (0) | 2023.10.16 |
| [Algorithm] BFS (0) | 2023.10.11 |
| Sort (0) | 2023.09.26 |

